Lesezeit 16 min.
Kapitel 1: Worum geht es im Prinzip?
Jeder Softwareentwickler stellt sich irgendwann in seiner Karriere einmal die Frage: "Warum habe ich nicht auf meine Mutter gehört und bin Arzt geworden?" Die Antwort darauf kennt auch nur die Studienplatzvergabe. Aber für alle anderen Fragen rund um die Ermittlung von Fehlerschwellen, sollte Dir dieser Blog Beitrag überaus nützlich sein. Oder Dir zumindest für Dein Problem, den Weg in die richtige Richtung zeigen. Solltest du also gerade z.B. eine Diagnose entwickeln, die Dir im Fehlerfall helfen soll, den Fehler zuverlässig zu erkennen oder du versuchst den richtigen timeout Wert zu ermitteln, dann bist du hier genau richtig. Denn die Auswahl solcher Werte kann manchmal tückisch sein.
Was passiert, wenn man hier nicht die nötige Sorgfalt walten lässt? Betrachten wir hier mal eine Diagnosefunktion. Hat man den zu ermittelnden Wert auf den Punkt genau ausgewählt, könnte es unter Normalbedingungen vorkommen, dass der Fehler gesetzt wird, obwohl dein System gar nicht fehlerhaft ist. Hier spielen verschiedene Faktoren wie Alterung oder Störgrößen eine entscheidende Rolle. Man spricht im Englischen von einem “False Failure” einem nicht berechtigten Fehlereintrag. Oder man wählt den Fehlerwert zu großzügig und erhält keinen Fehler, obwohl die System-Toleranzen bereits ausgeschöpft wurden. Hier spricht man von einem “False Pass”. Beides wird auf lang oder kurz zu Kundenbeanstandungen führen, da entweder andauernd ein unberechtigter Fehler angezeigt wird oder es wird kein Fehler angzeigt und das System nimmt ernsthaft Schaden. Es gilt beides gleichermaßen zu vermeiden. Für das bessere Verständnis habe ich ein reales Beispiel aus einem meiner Projekte herangezogen.
Nehmen wir eine Modbus Kommunikation zwischen einem Client und einem Server. Das Prinzip ist recht simpel, der Client fragt z.B. ein Register vom Server ab und erhält als Antwort die entsprechenden Werte aus dem Register. Wenn alles fehlerfrei funtkioniert.
Was tun wir aber, wenn der Server spät oder gar nicht antwortet? Oder eher gesagt, was macht unser System. Unser Code würde hier je nach Funktion endlos auf einen Receive-Interrupt warten oder ein Timer würde nach Ablauf die gesamte Funktion stoppen (Timeout). Der Timeout definiert also in der Programmierung eine fest definierte Zeitspanne, die ein Vorgang in Anspruch nehmen darf bis es zu einem Abbruch kommt um die weitere Funktionalität zu gewährleisten. Wie das Warten auf Godot und kleiner spoiler, nein, er ist niemals aufgetaucht. Ohne Timeout also würde unser System in einer Endlos-Schleife feststecken und auf eine entsprechende Antwort warten. Gut ich denke du hast das Prinzip des Timeouts verstanden. Aber wie lange sind wir bereit zu warten? Viele werden an dieser Stelle sagen: “Nimm 1 Sekunde als Timeout” und wahrscheinlich basiert
dieser Wert auf Erfahrungswerten, aber es gilt zu bedenken, dass die Timeout Zeit systembedingt variieren kann.
Und was ist, wenn wir auf Reddit oder StackOverflow keinen validen Timeoutwert finden können? Womit fangen wir an? Ist 42 eine gute Wahl? Long story short. Ein Testaufbau muss her. Schnell einen Trace gemacht und die besagte Antwort ist innerhalb von circa 30 ms da. Gut dann sollte unser FreeRTOS Timer wie folgt definiert sein:
handle_modbusTimeout_timer = xTimerCreate( "modbus_timeout", \
pdMS_TO_TICKS(30), pdTRUE, \
(void*)0, timeout_cb ); \
Jetzt stellt sich nur die Frage ob der ermittelte Wert auch representativ ist. Um das heraus zu finden sollten wir das System in verschiedenen Zuständen untersuchen und zwar in einer Art Dauerversuch. Hier kommt es immer darauf an, wie komplex Dein System ist und wie viele Störgrößen du identifizieren kannst. Um dich jetzt nicht gleich zu demotivieren, bleiben wir bei unserem Beispiel. Du identifizierst im wesentlichen zwei Hauptzustände des Server Systems:
Im folgendem etwas Theorie zur Datenerfassung. Die Datenerfassung ist der Prozess, bei dem Informationen systematisch gesammelt, aufgezeichnet und organisiert werden, um sie für Analysen, Berichte oder Entscheidungsfindungen zu nutzen. Sie kann in verschiedenen Formen erfolgen, darunter manuelle Eingabe, automatisierte Sensoren, Umfragen oder digitale Datenspeicherung. Die Qualität der Datenerfassung ist entscheidend, da sie die Grundlage für präzise Analysen und fundierte Entscheidungen bildet. In der heutigen datengetriebenen Welt spielt die Datenerfassung eine zentrale Rolle in Bereichen der Forschung und ermöglicht, Trends zu erkennen und Prozesse zu optimieren. Ganz in unserem Sinne also.
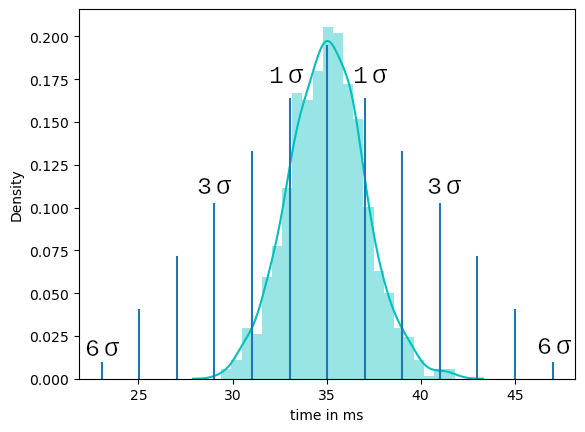
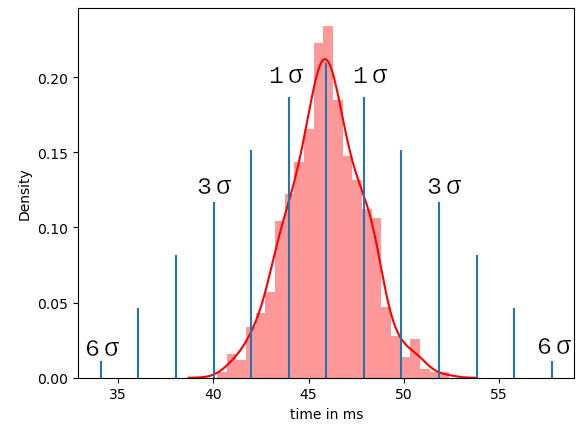
Für unser Beispiel messen wir also das Delta zwischen Client Request und Server Response. Zur besseren Differenzierung teilen wir die Datenerfassung in zwei Messungen auf. Die hier gesammelten Daten zeigen zunächst die Antwortzeit im Normalbetrieb. Anschließend nehmen wir eine zweite Messreihe auf mit einem simulierten Stress-Betrieb in dem wir beim Server einige Threads umpriorisieren und Art Dauerberechnungen hinzufügen und den Prozessor auslasten. Interrupts eignen sich an dieser Stelle auch recht gut. Bei Geräten in deinem Kommunikationsnetzwerk, auf die du keinen direkten Zugriff auf den Quellcode hast, wird es durchaus schwieriger. An dieser Stelle kann man zum Beispiel auf einer anderen Kommunikationsschnittstelle eine hohe Datenlast simulieren, indem man hohe Datenmengen über die entsprechende Schnittstelle schickt. Hierzu gibt es massenhaft verschiedene Herangehensweisen, auf die ich leider nicht in vollem Umfang in diesem Artikel eingehen kann. Darüber hinaus gibt es zahlreiche Software-Tools, die euch helfen können, System auszulasten. Aber manchmal reicht es auch schon, große Datenmengen über das Terminal zu schicken, um den besagten Effekt zu erzielen. Hier sind der Kreativität keine Grenzen gesetzt.
Der folgende Trace zeigt uns ein Beispiel aus dem Normalbetrieb zur besseren Vorstellung. Für die Messung benutze ich einen CH340 usb Adapter und ein selbstgeschriebenes Trace-Tool, was unter Linux recht einfach funktioniert und gleichzeitig das zeitliche Delta berechnet. Du benutzt Windows oder Mac? Auch hier gibt es massenhaft frei verfügbare Analyse-Tools. Da die Formatierung dieser Tools immer recht stark variiert, biete es sich an die Daten im so genannten post processing für unsere weitere Analyse aufzubereiten. Dies setze ich an dieser Stelle als gegeben voraus, da ich sonst den Rahmen des eigentlichen Themas sprenge.
Side Note:
Schau dir mal das Python Paket pandas genauer an. Hiermit ist eine Analyse der Datenreihe problemlos mit etwas Übung möglich. Wichtig ist nur, dass ihr das zeitliche Delta zwischen request und response vorliegen habt. Die hier verwendeten Daten sehen so aus und sind im csv Datei Format gespeichert:
13:24:02:4162, 0x03 0x02 0x00 0xc4 0x00 0x16 0xba 0xa9 || CRC: correct
13:24:02:4483, 0x03 0x02 0x03 0xac 0xbd 0x35 0x20 0x18 || CRC: correct
>> delta 32,1 ms
Du kannst die folgenden Daten als *.csv Datei abespeichern und dann mit dem in Kapitel 4 gezeigten Code auswerten:
30.5,34.4,32.9,32.0,36.5,34.1
,35.5,35.2,35.0,33.7,35.4,33.4
,34.9,37.9,33.7,33.9,34.1,35.3
,35.0,35.8,33.8,34.8,30.3,38.8
,34.6,32.9,34.8,33.3,35.3,30.9
,36.2,35.0,30.2,36.6,39.5,33.3
,35.0,38.6,33.6,33.7,33.9,37.0
,37.8,32.9,37.8,33.7,35.0,32.8
,37.9,35.1,35.9,35.9,34.8,37.7
,32.7,33.0,36.2,35.9,30.6,33.5
,34.4,32.4,35.4,37.6,35.4,34.6
Für die weitere Auswertung benötigen wir die folgenden python Pakete:
pip install matplotlib
pip install seaborn
Dann lesen wir die Daten ein und können anschließend das Histogramm und die Gauß'sche Normalverteilung berechnen. Wie im vorherigen Kapitel bereits erklärt, sollten wir die zwei Messungen nacheinander auswerten. Auf diese Weise kann man gut den Unterschied graphisch darstellen und muss sich nicht mit einer bimodalen Verteilung rumschlagen. Meine erfassten Daten liegen im *.csv Dateiformat vor und können mit dem folgenden Code eingelesen und verarbeitet werden.
import csv
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
x = []
with open('2024-10-8_Modbus_measurement_normal.csv', mode='r') as file:
filtered = (line.replace('\n', '') for line in file)
for line in filtered:
output_fromFile = line.split(",")
for elements in output_fromFile:
if (elements != ''):
x.append(float(elements))
sns.histplot(x, kde=True, color='c', fill=True, stat="density")
plt.show()
Nachdem wir die csv Daten eingelesen und unnötige Zeilenumbrüche und Leerzeichen entfernt haben, benutzen wir die Funktion histoplot() , welche uns das entsprechende Histogramm inklusive Normalverteilungskurve visualisiert. Der oben dargestellte Code enthält noch keine Sigma Trennstriche. Diese kasnnst du nach belieben mit dem folgenden Code optional anzeigen lassen.
deviation = np.std(x)
average = np.mean(x)
for i in range(1,7):
plt.axvline(x=(average - (i*deviation)), ymin=0, ymax=(0.9 - (i/7)))
plt.axvline(x=(average + (i*deviation)), ymin=0, ymax=(0.9 - (i/7)))
plt.axvline(x=(average), ymin=0, ymax=(0.85))
Nun zu den Fakten. Aus dem Histogramm können wir ablesen, dass der Mittelwert bei 35,03 ms liegt und die Standardabweichung gleich 1,997 ist. Gehen wir nun 6 sigma nach rechts in positiver x-Achse liegt unser Schwellwert bei 47,02 ms. Also würde die Wahrscheinlichkeit das ein beliebiger Wert in dem Wertebereich von -6sigma bis +6 sigma liegt, bei 99,9998% sein. Hört sich ziemlich sicher an, zumal wir den Bereich in negativer Richtung gar nicht abdecken möchten für unseren timout. Schneller kann zwar auch zu Fehler führen aber in unserem Fall nicht relevant. Gut, notieren wir also 47,02 ms und ziehen einen Timer von 50 ms für unseren timout mit entsprechender Callback auf. Die Callback bricht dann das Warten auf die Response Nachricht ab, so dass unser Programm weiter laufen kann.
handle_modbusTimeout_timer = xTimerCreate( "modbus_timeout", \
pdMS_TO_TICKS(50), pdTRUE, \
(void*)0, timeout_cb ); \
Laden wir nun aber die Daten der Stressmessung in unseren Python Code und setzen diese Daten ins Verhältnis, dann fällt schnell auf, dass ein Wert von 50 ms und größer durchaus beim Stresssystem vorkommen kann, und zwar mit einer Wahrscheinlichkeit von bis zu 5%. Jetzt haben wir uns die Mühe gemacht, die Daten aufzubereiten, auszuwerten und trotzdem ist unser System nur zu 95% robust. Was lernen wir hier also? Unsere Berechnungen sind nur so gut wie die dafür benutzen Messwerte.
Wir sehen also, wie stark äußere Einflüsse den Erwartungswert verändern. An dieser Stelle gibt es mehrere Möglichkeiten wie man das Stresssystem ins Verhältnis zum Normalsystem setzt. Aber um wirklich einen verlässlichen timeout Wert zu ermitteln sollten wir das Konzept des “worst-case-scenarios” anwenden. Bei diesem Risikomanagement Konzept wird das schlechteste Ergebnis für alle weiteren Berechnungen zu Grunde gelegt. In unserem Fall wäre dies, unsere Messreihen unter Spitzenlast. Werten wir sie mal aus und sehen uns die ermittelten Werte genauer an.
Der Mittelwert liegt nun bei 46,02 ms und die Standardabweichung beträgt 1,9754. Gehen wir wieder 6 sigma in Richtung positiver x-Achse liegt unser Schwellwert bei 57,78 ms. Suchen wir nur nun aus all unseren Messdaten die maximal gemessene Zeitverzögerung t_max, so erhalten wir einen Wert von 52,38 ms. Also hat uns Gauß doch nicht im Stich gelassen. Aber sind wir nun mit dem 57,78 ms timeout Timer über jeden Zweifel erhaben? Lasst uns zusammen die Gegebenheiten beleuchten und ich verspreche dir, es wird klarer.
An dieser Stelle möchte ich gerne näher auf unsere Betrachtungsweise eingehen. Vom mathematischen Vorgehen her, ist unsere Berechnung valide, aber dennoch ist der ermittelte Wert nur so gut und robust wie die Messdaten, aus denen er ermittelt wurde. Wir müssen also ein erhöhtes Augenmerk auf worst case Betrachtungen richten. Der Vollständigkeit muss gesagt sein, wir hätten gleich zu Anfang als Grundvoraussetzung für unseren Versuch alle möglichen Störgrößen identifizieren müssen, bevor wir unseren Versuch hätten starten dürfen. Selbst wenn die Normalverteilung von Carl Friedrich Gauß dir eine Wahrscheinlichkeit von 99,9998% gibt, ist dieser errechnete Wert nur so gut wie die Daten, aus denen er ermittelt wurde.
Kurzer Recap an dieser Stelle. Wir haben gelernt, wie wir Daten ermitteln und diese mithilfe der Mathematik und Python auswerten können. Dabei muss man einige Dinge beachten, wie die richtige Auswahl der Parameter für unseren Versuch. Aber auch die anschließende Auswertung ist wichtig. Am Ende steht man aber dennoch immer vor der Frage ob mal alle möglichen Szenarien berücksichtigt hat. Und leider muss ich Dir aus Erfahrung sagen, dass man trotz Worst case Betrachtung in der Entwicklung einem nachgelagerten Testing und Feldversuchen bei ausgewählten Kunden, immer wieder mit Fehlern überrascht wird, die man so nicht erwartet hätte.
Ich habe mir mal die Mühe gemacht auf Github und in diversen Foren nach Beispielen für einen Modbus timeout Wert zu suchen. Hier habe ich häufig einen Wert von 1000 ms gesehen. Dieser Wert ist um den Faktor 17,3 größer als unser ermittelter Wert von 57,78 ms . Warum ist das so? Zum einen haben wir hier stark isolierte Werte ermittelt, denn wir haben zum Beispiel nicht die verschiedenen Baudraten von 1200 bits per second bis 115200 bit per second betrachtet. Des Weiteren ist der hier untersuchte Aufbau nur für einen Server innerhalb eines Modbus Netzwerkes geprüft worden. Wie würden sich andere Server verhalten? Wie du schon merkst kommen immer mehr Varianzen auf und die gilt es mit einem Best Practice timeout Wert abzudecken. Da klingen die 1000 ms doch ganz passabel, vor allem wenn man die Einsatzzweck genauer betrachtet, aber dennoch muss man, um dies beurteilen zu können, erst einmal rechnen. Bei einem Airbag sind 1000 ms eine verdammt lange Zeit, aber beim Modbus hingegen verkraftbar. Unsere Aufgabe ist es, stets den Einsatzzweck im Auge zu behalten.
Damit sind wir auch am Ende und ich hoffe, du hattest Spaß beim Lesen.
Sie würden gerne Ihr aktuelles Projekt mit mir besprechen, dann schreiben Sie mir doch einfach eine E-Mail oder rufen mich an.
digitale Visitenkarte